Project #1

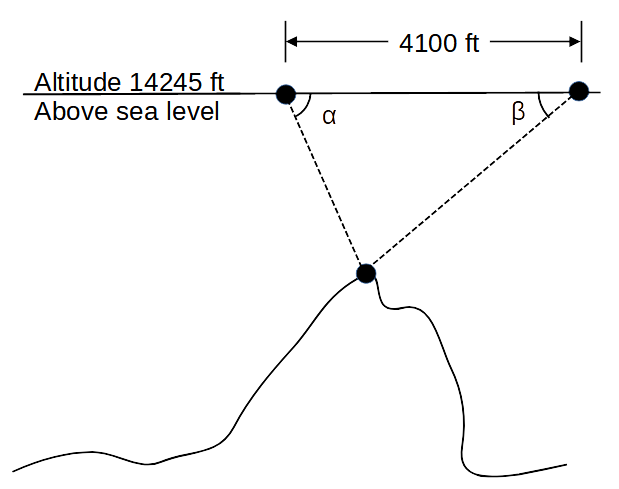
Assume you are flying in an airplane and you see a mountain. You think, "How high is that mountain?" Given you know your flight altitude and can fly directly over the mountain...

1. as you approach the mountain, you measure the angle (α) downward from the horizontal to the top of the mountain
2. after you pass over the top of the mountain, you measure the angle (β) downward from the horizontal to the top of the mountain again
3. calculate the distance between measuring point α and β
4. using the two angles and the distance between the two measuring points, calculate the height of the mountain
5. see the diagram below

Given
flight altitude	14,245 ft
measurement distance	4,100 ft
Angle α	41°
Angle β	36°

1. Calculate the third angle of the triangle

θ = 180 - α - β

2. Using the length of the side opposite the angle θ and the law of sines, calculate the length of the side opposite angle α

Lα = (sin(α) * 4100) / sin(θ)

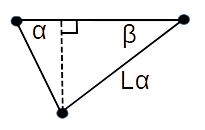
Vdistance = sin(β) * Lα

4. Calculate the mountain's height by subtracting the vertical distance from the flight altitude

Mheight = 14245 - Vdistance

Project #2

Create an interactive program. Let the user vary the input data.

These equations make no reality checks. With the right input data, you can be flying inside the mountain, or underground.

Project #3

Create an interactive program to draw a diagram (triangle) like the one in project #1. Ask the user to enter:

• flight altitude
• angle α
• angle β
• the distance between measuring point α and β

Calculate the "top-of-mountain" point. You will also need to scale the diagram (triangle) to fit the graphics window.

Use graphics.py to draw the diagram (triangle). Click HERE for more information. (download, install, documentation, ...)

What is sin and cos?

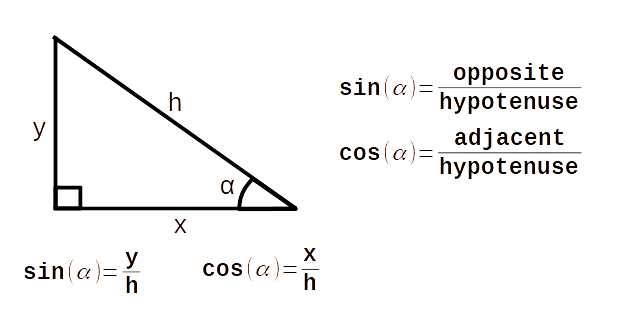
More Math Stuff (law of sines)

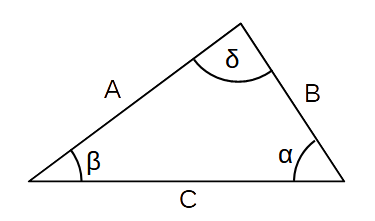
 sin(α)     sin(β)     sin(δ)
-------- = -------- = --------
   A          B          C

Use the Law of Sines to solve oblique triangles. Any triangle that is not a right triangle is an oblique triangle.

Note: There are three possible oblique triangle problem situations: ASA (angle-side-angle), AAS (angle-angle-side), and SSA (side-side-angle).

Links

More on the law of sines

Photogrammetry (Wikipedia)

Great Trigonometrical Survey (Wikipedia)

Greek Alphabet (Wikipedia)