Introduction
Convert galactic lat/lon found in a star catalog to X,Y,Z Cartesian coordinates. X,Y,Z coordinates can then be used to draw stars in a graphics window.
A star's galactic lat/lon is mapped to a sphere centered on the Sun. The sphere's radius of 1.0 which can be scaled. Note: On a galactic scale earth and sun are the same point.
Definitions from Wikipedia
Galactic longitude:
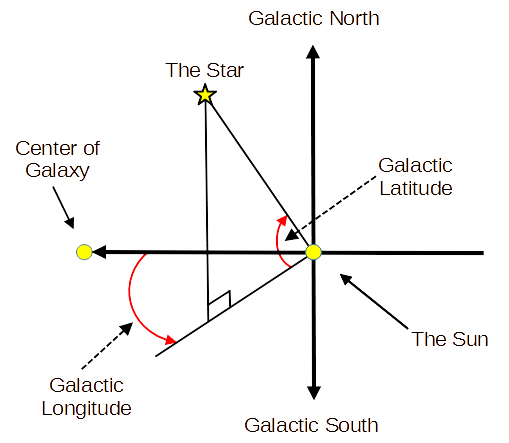
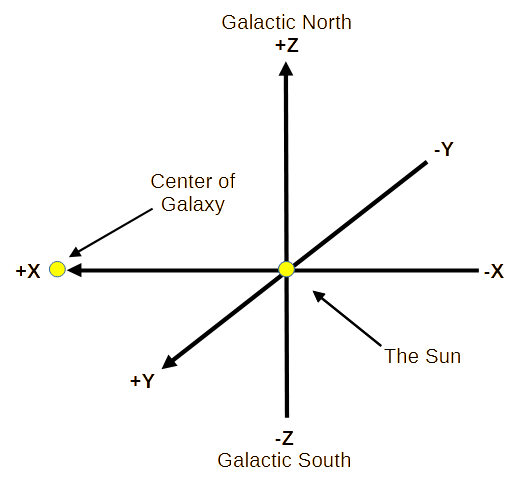
The galactic coordinates use the Sun as the origin. Galactic longitude (l) is measured with primary direction from the Sun to the center of the galaxy in the galactic plane. In rectangular coordinates the x-axis always goes to the center of the galaxy. Longitude measures the angular distance of an object eastward along the galactic equator from the Galactic Center. Viewed from the galactic north pole, eastward is counter-clockwise.
Galactic Latitude:
The galactic latitude (b) measures the angle of the object above the galactic plane. Latitude measures the angle of an object northward of the galactic equator (XY plane) as viewed from the Sun looking at toward the galactic center.
Simple Lat/Lon Conversion Test
#!/usr/bin/python
# ====================================================================
# test converting galactic lat/lon to x,y,z
#=====================================================================
import math as m
import user_interface as ui
description='''
=============================================================
test converting galactic lat/lon to x,y,z coordinates
-------------------------------------------------------------
Longitude is measured from the +x axis counter-clockwise
as viewed from the galactic north pole (0 to 360 degrees)
Latitude is measured from the galactic plane (the x,y plane)
+90 (north pole) to -90 (south pole)
-------------------------------------------------------------
-x (galactic anti-center)
(galactic north pole) +z /
| /
| /
|/
-y -------+------- +y
/|
/ |
/ |
/ -z (galactic south pole)
(galactic center) +x
-------------------------------------------------------------
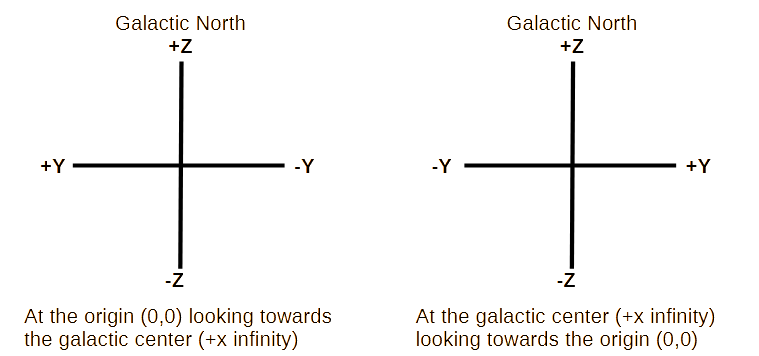
At the origin (0,0) looking towards the galactic
center (+x infinity)
+z
|
|
|
+y -------+------- -y
|
|
|
-z
-------------------------------------------------------------
At the galactic center (+x infinity) looking towards
the origin (0,0)
+Z
|
|
|
-y -------+------- +y
|
|
|
-z
-------------------------------------------------------------
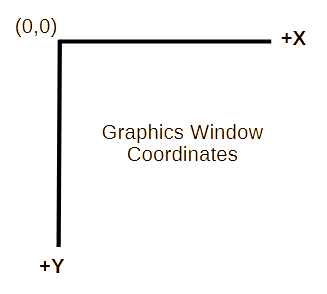
Graphics Window Coordinates
(0,0) +-------------- +x
|
|
|
|
|
+y
=============================================================
'''
# --------------------------------------------------------------------
# ---- convert radians to deg,min,sec
# ---- note: 1 radian equal to 57.296 degrees
# --------------------------------------------------------------------
def convert_radians_deg_min_sec(rad):
totalSeconds = int(round(rad*360*60*60/(2*m.pi)))
sec = totalSeconds % 60
min = (totalSeconds / 60) % 60
deg = totalSeconds / (60 * 60)
## print(f'rad = {rad:.3f} deg,min,sec = {deg},{min},{sec}')
return(deg,min,sec)
# --------------------------------------------------------------------
# ---- convert Cartesian x,y,x to galactic lat/lon
# ---- x,y,z are for point on the sphere of stars
# ----
# ---- return angles in degrees and radians
# ---- note: the radius of sphere of stars is 1.0
# --------------------------------------------------------------------
def convert_xyz_to_lat_lon(x,y,z):
r = 1.0 # radius of sphere of stars
lat = m.asin(z/r) # latitude (radians)
lon = m.atan2(y,x) # longitude (radians)
return (m.degrees(lat),m.degrees(lon),lat,lon)
# --------------------------------------------------------------------
# ---- convert galactic lat/lon (degrees) to x,y,x
# ---- note: the diameter of sphere of stars is 1.0
# ---- viewer is at +x infinity
# --------------------------------------------------------------------
def convert_lat_lon_to_xyz(lat_deg,lon_deg):
lat_rad = m.radians(lat_deg) # radians
lon_rad = m.radians(lon_deg) # radians
x = m.cos(lat_rad) * m.cos(lon_rad)
y = m.cos(lat_rad) * m.sin(lon_rad)
z = m.sin(lat_rad)
return (x,y,z)
# --------------------------------------------------------------------
# ---- main
# --------------------------------------------------------------------
viewer = '''
---------------------------------------------
Viewer is at the galactic center (+x infinity)
looking towards the origin (0,0). (The sun.)
---------------------------------------------'''
print(description)
while True:
print()
print(viewer)
s = ui.get_user_input('Enter star\'s galactic lat/lon: ')
if not s: break
s = s.replace(',', ' ')
s = s.replace(r'/', ' ')
s = s.replace(':', ' ')
slat,slon = s.split()
tf,lat = ui.is_float(slat)
if not tf:
print('bad latitude entered')
continue
tf,lon = ui.is_float(slon)
if not tf:
print('bad longitude entered')
continue
x,y,z = convert_lat_lon_to_xyz(lat,lon)
print()
print(f'lat/lon = {lat:.2f}/{lon:.2f} ' +
f'x = {x:.2f} y = {y:.2f} z = {z:.2f}')