Chauvenet’s Criterion

The following is from Chauvenet’s Criterion

The procedure assumes your data is normally distributed.

Chauvenet’s criterion is a way to identify outliers. The method works by creating an acceptable band of data around the mean. Eliminate any value that fall outside of the band.

Assuming you have a random sample of n values

1. Find the sample's mean (m)


2. Find the sample's standard deviation (s)


3. Use the following formula to find the standardized deviation from the mean for each value in the sample

   

   Run the formula n times (One time for each data point).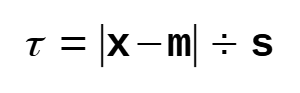

Compare the value you get with the tables of Chauvenet’s criterion below. Reject values that exceed the criterion.

For example if n=30, the table tells us a value's standard deviation should not exceed 2.394. If it does reject it.

If you’ve find an abnormal amount of outliers, you might want to widen the band to include a certain percentage of data points. The empirical rule tells us that 95% of data lies within two standard deviations from the mean. Therefore you should eliminate a maximum of 5% of your data points.

n	τ
3	1.383
4	1.534
5	1.645
6	1.732
7	1.803
8	1.863
9	1.915
10	1.960
11	2.000
12	2.037

n	τ
13	2.070
14	2.100
15	2.128
16	2.154
17	2.178
18	2.200
19	2.222
20	2.241
21	2.260
22	2.278

n	τ
23	2.295
24	2.311
25	2.326
26	2.341
27	2.355
28	2.369
29	2.382
30	2.394
31	2.406
32	2.418

n	τ
33	2.429
34	2.440
35	2.450
36	2.460
37	2.470
38	2.479
39	2.489
40	2.498
50	2.576
100	2.807

n	τ
500	3.291
1000	3.481

Note: Deletion of outlier data is a controversial practice frowned on by many scientists and science instructors; while Chauvenet's criterion provides an objective and quantitative method for data rejection, it does not make the practice more scientifically or methodologically sound, especially in small sets or where a normal distribution cannot be assumed. Rejection of outliers is more acceptable in areas of practice where the underlying model of the process being measured and the usual distribution of measurement error are confidently known.
Chauvenet's criterion (Wikipedia)