Introduction
A binary tree is a tree data structure in which each node has at most
two children. They are referred to as the left child and the right child.
(Wikipedia)
The left node is always less than its parent node.
The right node is always greater than its parent node.
Note:
- The nodes at the end of a branch are called "leaf" nodes.
- For this exercise/program only use integers.
(This will simplify things for now.)
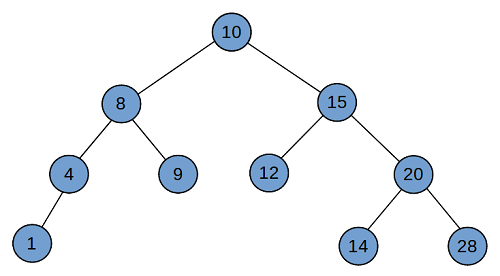
A balanced binary tree, also referred to as a height-balanced binary tree,
is defined as a binary tree in which the height of the left and right
sub-trees of any node differ by not more than 1.
(Wikipedia)
Do not uses any existing Python module/package "that does" binary trees.
The purpose of these projects is to "do them" yourself.
However, using code found on the web or in a book is legal. (See the links below.)
Project #1
Create and interactive program to create a Binary Search Tree (BST)
The program will build and maintain a binary tree of integers
(integers: 0 to 999)
- insert a value (what to do with duplicates?)
- search for a value
- delete a value
- delete the binary tree
- ask the user for a string containing CSV values and
insert the values into the tree
- display the tree's nodes
- display the tree
Insert the following values (in the order shown) into a BST.
[ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ]
What does the binary tree look like?
What order of input would create the binary tree in the diagram above?
Project #2
Balance a Binary Search Tree (BST).
Is there a Python module or an algorithm you can use?
Example 1
Unbalance tree (laid on it's side)
---------------- 501
------------ 500
---------------- 499
-------- 456
---- 45
-------- 40
23
-------- 12
---- 11
-------- 8
Balance tree (laid on it's side)
---------------- 501
------------ 500
---- 499
------------ 456
-------- 45
40
------------ 23
-------- 12
---- 11
-------- 8
Example 2
Unbalance tree (laid on it's side)
-------------------------------- 9
---------------------------- 8
------------------------ 7
-------------------- 6
---------------- 5
------------ 4
-------- 3
---- 2
1
Balance tree (laid on it's side)
------------ 9
-------- 8
---- 7
-------- 6
5
------------ 4
-------- 3
---- 2
-------- 1
Code Hint
# --------------------------------------------------------------
# ---- tree node class
# ----
# ---- Traditionally the child nodes of a parent node are named
# ---- left and right. Left is a sub-tree that contains all of
# ---- node less than the parent node. Right is a sub-tree
# ---- that contains all of the nodes (and equal) to the
# ---- parent node.
# --------------------------------------------------------------
class Node():
def __init__(self,value):
self.value = value # node value
self.parent = None # parent node
self.left = None # left child
self.right = None # right child
More Hints
Links
binary Tree (Wikipedia)
B-tree (Wikipedia)
Self-balancing binary search tree (Wikipedia)
Python - Binary Tree
Convert a Binary Search Tree (BST) to a Balanced BST
Self-Balancing Binary Search Trees
