Hodgepodge

Project #1

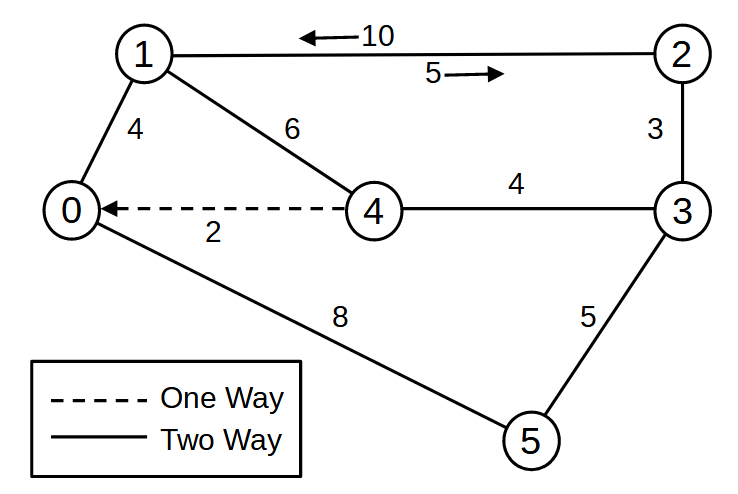
image mising

Create a compact cost matrix of the diagram and write it a file so it can be read and used by other programs. (CSV? JSON? ...)

This diagram (graph) is a hypothetical freeway system with construction on one link slowing traffic in one direction. Another links has no connection in one direction. (detour?)

Why save it to a file? Suppose you are doing this for a large metropolitan area.

it might contain thousands of nodes

it changes slowly

everyone is using the same data

The compact cost matrix should have the following format

# ---- compact cost data # from_id is a matrix row index # to_id is a matrix column index # cost is the cost from_id to to_id compact_costs = [ [from_id, [(to_id,cost),(to_id,cost)], 'Home'], [from_id, [ ....................... ], None], [from_id, [ ....................... ], 'Shopping'], ... ... ] Read this as, row (id) to outbound connection column (id). For example, source node 1 to destination node 2 has a cost of 5. Source node 2 to destination node 1 has a cost of 10. Each row in the compact cost data contains 3 items

item	description
0	row (node) index (redundant and not used.) it is there to make it easier for humans to read the data.
1	a list of outbound connections. it contains outbound (destination) nodes and their node-to-node costs.
2	node name if any (just for important nodes.)

The compact cost data is from-node (row index) --> to-node (column index). The graph designer only needs to think about outbound connections.

The matrices are from-node (column) --> to-node (row). This is especially useful for the minimum paths matrix. All of the minimum paths to a given node are in a single row. You don't need to bounce around inside of a 2D matrix.

Project #2

Write a program that reads a compact cost matrix file and creates a regular cost matrix. (Put this in a function so it can be used by other programs?)

Programming hint: create a 2D matrix filled with -1. Next fill it with costs from the compact cost matrix data.

Project #3a

Create a program that uses Dijkstra's algorithm and the data generated in Problem #2. Create a 2D minimum path matrix. Save it to a file?

There are many descriptions of the algorithm on the web and also many code examples on on the web. Use (and modify) the algorithm to create a minimum path matrix.

Display the minimum path matrix in a pretty way. (See this project's root page.)

Project #3b

Calculate an accumulative (node-to-node) cost matrix.

Display the accumulative (node-to-node) cost matrix in a pretty way. (See this project's root page.)

Project #4

Generate a random 2D graph with at least 50 nodes.

each node has 2 to 4 outbound connections (or 1 connection as long is not a one way connection)
there a few one way connections (5%?)
the connection cost of a few of them is not the same in both directions (2%?)
the cost of each node-to-node connection is randomly generated (1 to 20?)

Testing hint: Test using 4 or 5 random nodes (use a seed) until it is working. Lastly generate a big one.

This is not required. The locations (coordinates?) for each node could also be randomly generated. How do you draw/plot this diagram (graph)?

Project #5

Do it all over again in 3D. (Create a 3D cost matrix.)