A Version of Dijkstra’s Algorithm From the Web
This demo code is from the website:
www.geeksforgeeks.org/shortest-paths-from-all-vertices-to-a-destination/

Notes about the code
- The code uses the PriorityQueue from the queue module. Here are some links to help you get started.
- The code has a need for an integer infinity. Instead it uses a very large
integer value as infinity. In this code that is good enough.
Using an integer to represent infinity violates the definition of infinity. As far as I know, there is no way to directly represent infinity as an integer number. However, in Python numbers are objects and Python has a way to represent infinity. For example:
Note: Infinity can be both positive and negative. import math x = math.inf if math.isinf(x): print(f'math: {x}) is infinity') y = -math.inf if math.isinf(y): print(f'math: ({y}) is infinity') import numpy as np x = np.inf if np.isinf(x): print(f'np: ({x}) is infinity') y = -np.inf if np.isinf(y): print(f'np: ({y}) is infinity')
Note: to check for positive and negative infinite, check if the number is greater than 0 or less than 0.
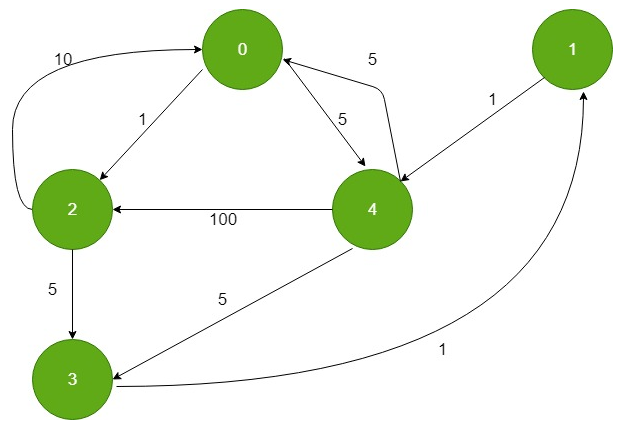
Test graph used by the code
Python code from the website
#!/usr/bin/python3
from queue import PriorityQueue
INF = int(0x3f3f3f3f)
# This class represents a directed graph using
# adjacency list representation
class Graph:
def __init__(self, V: int) -> None:
self.V = V
# No. of vertices
# In a weighted graph, we need to store vertex
# and weight pair for every edge
self.adj = [[] for _ in range(V)]
def addEdgeRev(self, u: int, v: int, w: int) -> None:
self.adj[v].append((u, w))
# Prints shortest distance from all vertex to
# the given destination vertex
def shortestPath(self, dest: int) -> None:
# Create a priority queue to store vertices that
# are being preprocessed. This is weird syntax in C++.
# Refer below link for details of this syntax
# https:# www.geeksforgeeks.org/implement-min-heap-using-stl/
pq = PriorityQueue()
# Create a vector for distances and initialize all
# distances as infinite (INF)
dist = [INF for _ in range(V)]
# Insert destination itself in priority queue and initialize
# its distance as 0.
pq.put((0, dest))
dist[dest] = 0
# Looping till priority queue becomes empty (or all
# distances are not finalized) */
while not pq.empty():
# The first vertex in pair is the minimum distance
# vertex, extract it from priority queue.
# vertex label is stored in second of pair (it
# has to be done this way to keep the vertices
# sorted distance (distance must be first item
# in pair)
u = pq.get()[1]
# 'i' is used to get all adjacent vertices of a vertex
for i in self.adj[u]:
# Get vertex label and weight of current adjacent
# of u.
v = i[0]
weight = i[1]
# If there is shorted path to v through u.
if (dist[v] > dist[u] + weight):
# Updating distance of v
dist[v] = dist[u] + weight
pq.put((dist[v], v))
# Print shortest distances stored in dist[]
print("Destination Vertex Distance from all vertex")
for i in range(V):
print("{} \t\t {}".format(i, dist[i]))
# Driver code
if __name__ == "__main__":
# create the graph given in above figure (see webpage)
V = 5
g = Graph(V)
# adding edges in reverse direction
g.addEdgeRev(0, 2, 1)
g.addEdgeRev(0, 4, 5)
g.addEdgeRev(1, 4, 1)
g.addEdgeRev(2, 0, 10)
g.addEdgeRev(2, 3, 5)
g.addEdgeRev(3, 1, 1)
g.addEdgeRev(4, 0, 5)
g.addEdgeRev(4, 2, 100)
g.addEdgeRev(4, 3, 5)
g.shortestPath(0)
# This code is contributed by sanjeev2552
---- code generated values -----------------------------------------
Output : 0 6 10 7 5
Distance (cost) of 0 from 0: 0
Distance (cost) of 0 from 1: 1+5 = 6 (1->4->0)
Distance (cost) of 0 from 2: 10 (2->0)
Distance (cost) of 0 from 3: 1+1+5 = 7 (3->1->4->0)
Distance (cost) of 0 from 4: 5 (4->0)
---- or in my format -----------------------------------------------
# [0] [1] [2] [3] [4] (col is from-node)
#
minimum_paths = [ [ 0, 4, 0, 1, 0 ], # row is to-node [0]
[ ... ], # row is to-node [1]
[ ... ], # row is to-node [2]
[ ... ], # row is to-node [3]
[ ... ] ] # row is to-node [4]
#
#
# [0] [1] [2] [3] [4] (col is from-node)
#
accumulated_costs = [ [ 0, 6, 10, 7, 5 ], # row is to-node [0]
[ -1, 0, -1, -1, -1 ], # row is to-node [1]
[ -1, -1, 0, -1, -1 ], # row is to-node [2]
[ -1, -1, -1, 0, -1 ], # row is to-node [3]
[ -1, -1, -1, -1, -1 ], # row is to-node [4]
[ -1, -1, -1, -1, 0 ] ] # row is to-node [5]