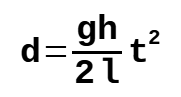Galileo's Measurement Of Gravity
Test Code

Introduction

Galileo hypothesized that a falling object would gain equal amounts of velocity in equal amounts of time, which meant that as it fell its speed increased at a constant rate. His experiments proved this to be true.

Galileo described his experiment in his book "Discourses on Two New Sciences" (1638).

Note: Roll a ball down a ramp. If you doubled the amount of time that the ball rolls, it travels four times as far.

Gravity

The acceleration of gravity on earth is approximately

Note: Gravity varies on the surface of Earth, because of the size of Earth and the distance we are on its surface from its center. Also the density of the Earth varies in different places.

For these projects use 9.8 m/sec/sec or 32 ft/sec/sec for the acceleration of gravity.

Project #1

Questions:

  1. what is the difference between speed and velocity (if any)?

  2. the earth is not perfect sphere. What is its shape? (Hint: It is an oblate ...)
    (The answer is at the bottom of this webpage)

Project #2

Create a graphics simulation of Galileo's experiment. It should include

Use graphics.py. Click HERE for more information. (download, install, documentation, etc.)

Project #3

Allow the user to select the acceleration of gravity

Sun274.13 m/sec2
Mercury3.59 m/sec2
Venus8.87 m/sec2
Moon1.62 m/sec2
Mars3.77 m/sec2
Jupiter25.95 m/sec2
Saturn11.08 m/sec2
Uranus10.67 m/sec2
Neptune14.07 m/sec2
Pluto0.42 m/sec2

If you change the gravity and the time jump remains the same as Earth's gravity experiment, the distance the ball travels will change.

Links

Galileo's Inclined Plane Experiment
Galileo's Measure Of Gravity Explained By Jim Al-Khalili (YouTube)
Making a gravity simulator using Python
Create Your Own N-body Simulation (With Python)
Problem with simulating gravity in Python

Distance Traveled

image missing
Equation from HERE
d distance traveled by the object
h and l are the height and length of the inclined plane
g gravitational acceleration
t time

The answer to the shape of the earth is

YMJ JFWYM NX F UJFW XMFUJI TGQFYJ XUMJWJTNI
See the project "Send and receive secret messages" to see how to decrypt the answer.

The encryption shift factor is 5. The character set is: 

abc = ['A', 'B', 'C', 'D', 'E', 'F', 'G', 'H', 'I', 'J',
       'K', 'L', 'M', 'N', 'O', 'P', 'Q', 'R', 'S', 'T',
       'U', 'V', 'W', 'X', 'Y', 'Z', '.', '?', '!', '(',
       '1', '2', '3', '4', '5', '6', '7', '8', '9', '0',
       ')']

Useful Formulas

Finds the distance traveled (d) of an object with an initial velocity of zero, acceleration (a), and time (t) traveled. The equation used is 

d = ½ * a * t2

Finds the distance traveled (d) of an object with an initial velocity (v), acceleration (a), and time (t) traveled. The equation used is 

d = (v * t) + (½ * a * t2)

How it Works

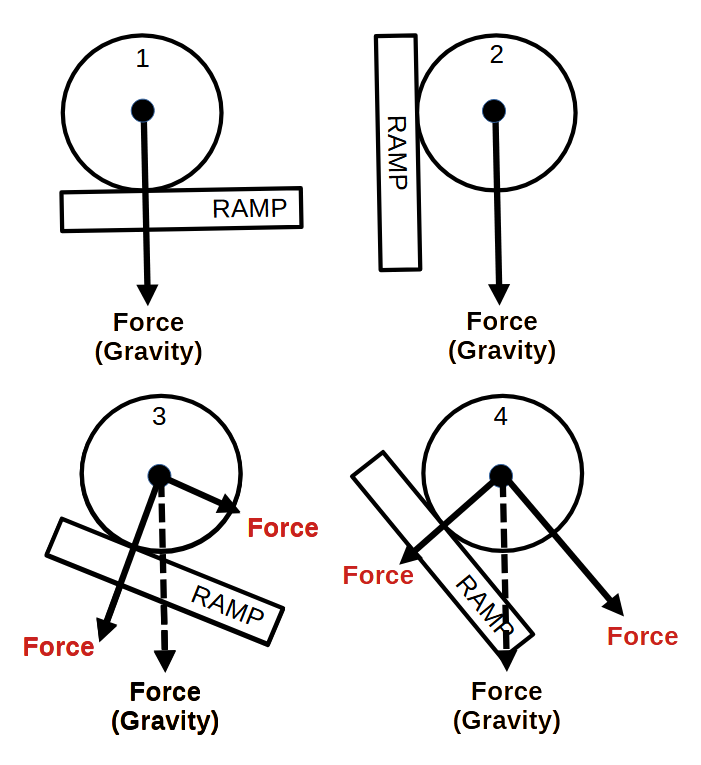
image missing

In the examples above the ball is pulled by the force of gravity. As you can see in the diagram the force of gravity is downward.

In the first example the ramp is resisting the force of gravity on the ball. The ball does not move because there is no sideways force. The force of gravity pulls (tried to accelerates) the ball but the ramp pushes back.

In the second example the ramp is not in a position to resist the force of gravity on the ball. The full force of gravity pulls (accelerates) the ball downward.

In the third and forth examples the ramp is at an angle to the ball. The force of gravity can be defined as two independent forces. One force is pushing the ball against the ramp. The other force pulls (accelerates) the ball down the ramp. (Note: The sum of the two forces equals the force of gravity.)

By adjusting the steepness of the ramp you can control how fast the ball accelerates. The steeper the ramp the fast the ball is pulled (accelerated) down the ramp.

Remember F = M*A   (The bigger the force the faster the acceleration.)

Firesign Theatre - circa 1971 (Just for Fun)

{Fudd's First Law}: If you push something hard enough it will fall over.