Introduction

Lets break down the problem into manageable parts.

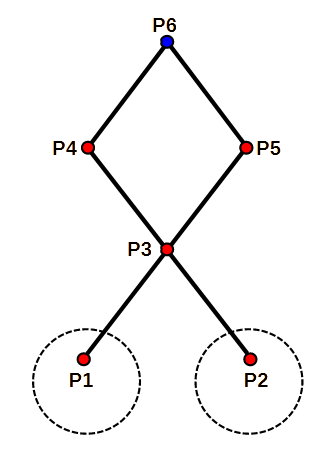
1. label every point so we can keep track of them in the math
2. determine which coordinate system to use
3. determine the center of the wheels and the initial rotation angle
4. loop
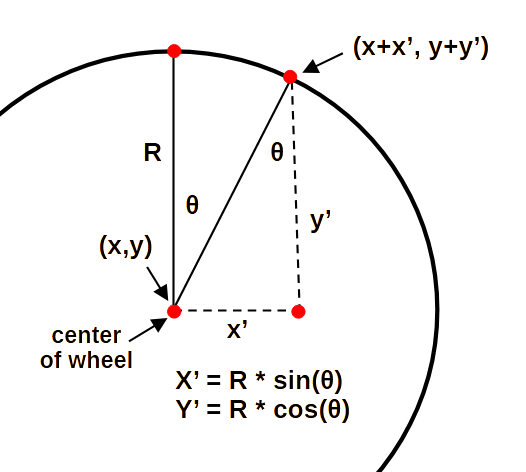
   1. find the coordinates of P1 and p2
   2. find the coordinates of P3
   3. find the coordinates of P4 and P5
   4. find the coordinates of P6
   5. draw p6 in the graphics window
      • convert the coordinates to window coordinates
      • draw the point
   6. rotate the wheels

Initial Assumptions

1. wheel centers are at (-40,-100) and (40,-100)
2. both wheels rotate at the same speed and angle
3. wheels rotate clockwise
4. wheel starting rotation angle (0^°) is straight up
5. assume P1 and P2 start directly over the center of the wheels
6. define the coordinates of P1 and P2 attached to the edge of the wheels
7. radius of the wheels is 30
8. center of the wheels are 80 apart
9. center of the wheels are on the same level (same y coordinate)
10. P1-to-P5 is 100 and P2-to-P4 is 100
11. P1-to-P3 is 50 and P2-to-P3 is 50
12. P4-to-P6 is 50 and P5-to-P6 is 50

These assumptions are a place to start and undoubtedly will need changing as we test and learn more.

Label Each Point

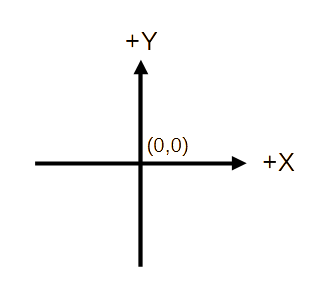
Coordinates

I suggest trying Cartesian coordinates with the origin at the center of the graphic window.

Coordinates of P1 and P2

Coordinates of P3

Use the Law of Cosines and the Pythagorean Theorem.

Coordinate of P4 and P5

Use similar triangles.

Coordinates P6

Use the law of Cosines and the Pythagorean Theorem.