Introduction

The Monte Carlo method can be used to estimate the area of an irregular shape. The unknown shape (area) is placed inside a known shape (area). Random points are generated in the known shape (area). Some will fall inside the irregular shape and some will not. Using the counts we can estimate the size (area) of the irregular shape.

The main problem is "how do you count the points inside and outside an irregular shape?" Unless it is automated, counting a large number of random points is a daunting task. Not impossible, just daunting.

Definition: The Monte Carlo method is a mathematical technique that uses a large number of randomly generated numbers to get an approximate solution to a problem that would be difficult to solve by other methods. It is named after the Monte Carlo resort famous for its gambling casino.

Project #1

In this project we will verify/test the accuracy of the Monte Carlo method.

We will test it using known shapes (areas). They are a circle in a square. A point's distance for the center of the circle can be used to determine if it is inside or outside the circle.

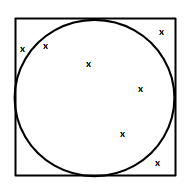
The Monte Carlo method is accurate within certain limits. Test the following number of random points and plot the results (known vs calculated).

• 50 random points
• 100 random points
• 500 random points
• 1000 random points
• 5000 random points
• 10000 random points
• 15000 random points
• 20000 random points

There is probably a point of diminishing return as the number of random points increase. (The accuracy growth is not linear?)

Perform each test 10 times and average the results. This will help smooth out the random results. (Do the test 100 times? Draw a bell curve of the test results. Is 100 times better?)

Plot the accuracy of the Monte Carlo method vs the random point counts. Accuracy is the percent difference between the know area and the calculated (estimated) area of the circle. The plot will allow a user to estimate the number of random points to use to get the accuracy they need.

Create two programs. The first program generates the data and save it to a file. The second program read the file and draws the plot.

Assumptions:

• The length of a side of the square is 100.
• Increasing the number of random points increases the accuracy.
• The area of the circle is known.
• The area of the square is known.
• The center of the square is also the center of the circle.
• If the method accurately estimates the area of a known shape, it will be accurately estimate the area of an unknown shape.

Use pyplot or other plot module. For more information about matplotlib.pyplot click HERE .

Project #2

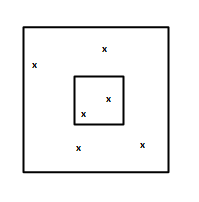
Do project #1 but with a square inside a square. the inside square's side is one third the outside square's side. (The length of a side of the outside square is 100.)

The inside square represents an unknown shape.

Project #3

Will using a larger box size compared to the circle inside increase the accuracy?

Experiment with

• square_side = 100, circle_radius = 50
• square_side = 200, circle_radius = 50
• square_side = 300, circle_radius = 50
• square_side = 400, circle_radius = 50
• square_side = 500, circle_radius = 50

Run each experiment 1000 times and average the results. Use 10,000 random points for each experiment.

Calculate the mean and standard deviation

• Plot the mean vs box size (area)
• Plot the standard deviation vs box size (area)
• Plot the ratio of box area to circle area

Does having the area outside of the circle be approximately the same size of the circle improve accuracy? Is bigger better?

Project #4

Create a graphics program showing the random points as they are created.

Use graphics.py. For more information click HERE . (download, install, documentation, etc.)

Equations, etc.

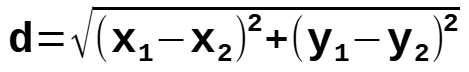The distance between two points: d = distance between points p₁ = x₁,y₁ p₂ = x₂,y₂

Is A Point Inside or Outside the Circle?

Given a random point inside the square

1. Calculate the distance between the point and the center of the circle.
2. Is the distance less than or greater than the circle radius?

What do you do if the distance is exactly the radius?

Links

Estimating the area by throwing random points

How to calculate the area of bizarre shapes

What is the Monte Carlo method for areas?

The essence of the Monte Carlo method is very simple. If we allocate points randomly within a square the ratio of the areas of a circle and a square is equal to the ratio of the number of points N₀ (that fall into a circle) and the total number of points N₁: The larger the area, the more points it gets.
From How does the Monte Carlo method work? (pdf)

Some thoughts on irregular shapes and the Monte Carlo method