Hodgepodge

Introduction

This is not a course in statistics. It is an introduction to a simple linear regression methodology. There is a lot more to learn about statistics and regression, but not here.

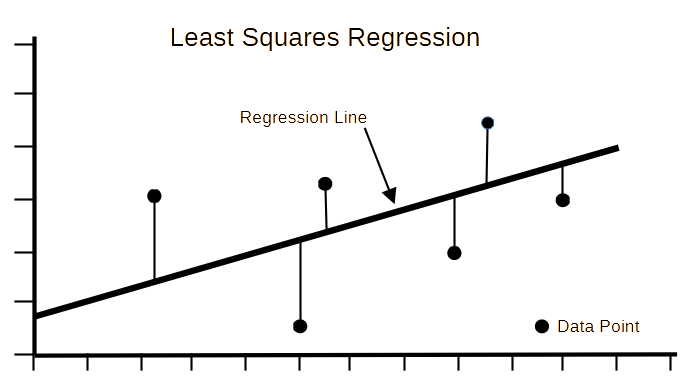
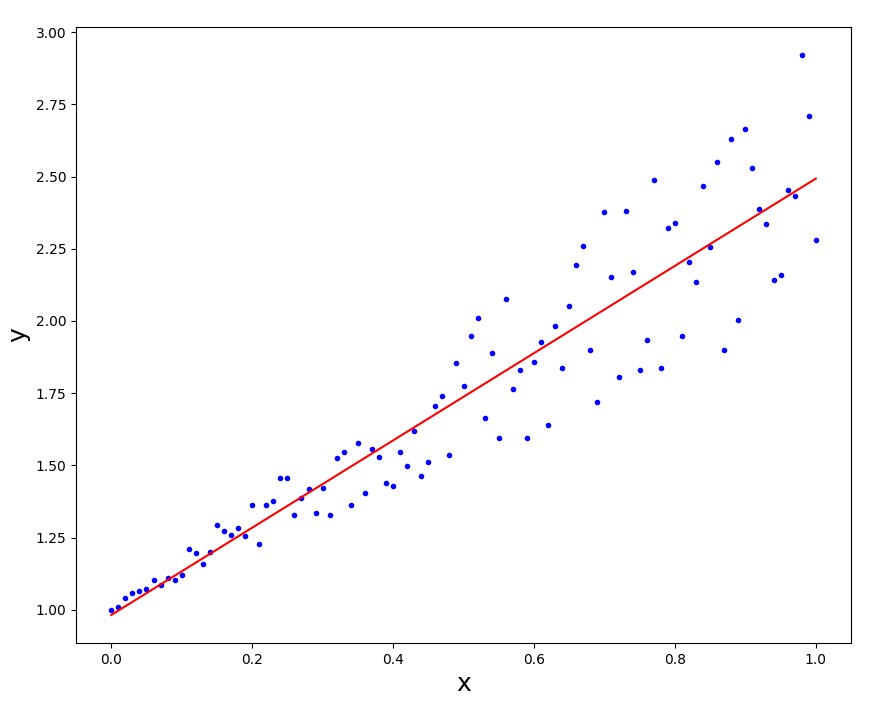
image missing

The diagram shows the data points that were measured/collect for analysis.

The regression line is a theoretical line describing the data points. If the data was perfect the data points would fall directly on the line. Because the data is not perfect, mathematical methods (e.g. least squares regression) can be used to find the Line-of-Best-Fit. The line minimizes the sum of the distances from data points to the theoretical perfect line.

The point of all of this is to get the equation for the perfect line that can be used to predict other (dependent) values.

We can also measure how badly the data points fit the perfect line. However, that problem is not part of this project.

Do not use any existing Python modules, etc. Use/code the equations show below.

Project #0

Create test data for Project #1.

One way is to use this code

import numpy as np # to generate the same set of random # number for testing # set a seed value (do not use 0) np.random.seed(2001) # generate x and y data x = np.linspace(0,1,101) y = 1 + x + x * np.random.random(len(x))

Another way is to use data from one of the following

10 open datasets for linear regression

To plot the data I suggest you use the pyplot or related modules.
matplotlib.pyplot . (documentation and examples)
To see more random data generation and pyplot examples click HERE .

Data Assumptions

There are limitations when using the Least Squares method.

It only defines the relationship between the two variables.
Other causes and effects are not considered.
The variables measured should be continuous.
For example time, sales, weight, test scores ...
Observations should be independent of each other.
There should be no dependency.
It is unreliable when data is not evenly distributed.
Data should have no significant outliers.

Note: You can use a scatter plot to identify a possible relationship between two different sets of variables.

Project #1

In this project, you will run a simple demo of regression analysis using the Least Squares method. Create a program to

Read x,y data points from a file.
Find the theoretical perfect line.
Plot the data points and the line.

To plot the data I suggest you use the pyplot or related modules.
matplotlib.pyplot . (documentation and examples)
To see more random data generation and pyplot examples click HERE .

Equation of a Line

The 'x' (independent variable) values are used to calculate the 'y' (dependent variable) values. In other words, using the equation, 'x' can be used to calculate 'y'.

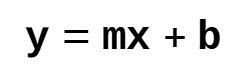y: dependent variable m: the slope of the line x: independent variable b: y-intercept

Steps to Calculate the Line-of-Best-Fit

The following steps calculate the values of slope and y-intercept for the Line-of-Best-Fit (the regression line).

You can use the following two tests to verify your code is working correctly. Then use the data you generated.

test #1 data and results m = 1.5182926829268293 b = 0.30487804878048674 x = [2,3,5, 7, 9] y = [4,5,7,10,15]

test #2 data and results m = 2.8 b = 6.2 x = [1, 2, 3, 4, 5] y = [7,14,15,18,19]

Programming hint

Lookup the Python sum function

For each (x,y) calculate x² and xy

Sum x, y, x² and xy (i.e. ∑x, ∑y, ∑x², and ∑xy)

Calculate the slope (m) using the equation in step 1

Step 1: Calculate the slope 'm'

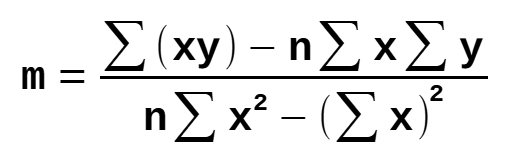y: dependent variable x: independent variable n: number of data points

Step 2: Calculate the y-intercept

The 'y' value where the line crosses the y-axis. (i.e. x = 0)

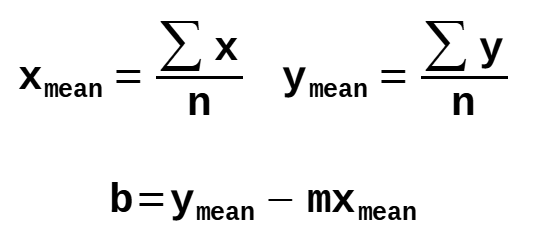y: dependent variable m: the slope of the line x: independent variable b: y-intercept

Step 3: Substitute the values to get the final equation

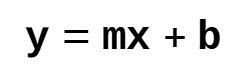y: dependent variable m: the slope of the line x: independent variable b: y-intercept

Definitions

Math Term	Definition
Dependent variable	a variable (often denoted by y) whose value depends on that of another.
Independent variable	a variable (often denoted by x) whose variation does not depend on that of another.
Least Squares Regression	The Least Squares Regression Line is the line that minimizes the sum of the residuals squared. The residual is the vertical distance between the observed point and the predicted point, and it is calculated by subtracting Y_predicted from Y_observed.

Example Plot

image missing

Links

A 101 Guide On The Least Squares Regression Method

Linear Regression Algorithm In Python From Scratch [Machine Learning Tutorial] (YouTube)

Least Squares Regression in Python

Solving Linear Regression in Python

Linear regression (disambiguation) (Wikipedia)

Least-Squares Fit to a Straight Line python code

Least Squares Regression