This square root algorithm is known as Heron's method, after the first-century Greek mathematician Hero of Alexandria. This method is also called the Babylonian method.

Given a positive real number S, let X₀ > 0 be any positive initial estimate. The algorithm consists of iteratively computing the square root until the desired accuracy is achieved.

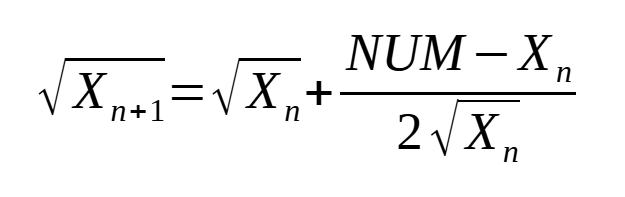
NUM	the number we want the square root of
√Xn	the previous loop's estimated square root of NUM Note: the initial value (X0) is the "nearest perfect square" to NUM
√Xn+1	the new estimate of the square root of NUM
Xn	√Xn**2

This algorithms require an initial seed value (initial estimate). Use the "nearest perfect square" as the seed.

Note: If the seed is far away from the square root being calculated, the algorithm will require more iterations.

FYI

The Babylonian method for finding square roots by hand