Polar Coordinates

Polar coordinates define a point's location using a distance from a reference point and a counterclockwise angle from a reference direction.

1. The reference point is the origin (0,0) of Cartesian coordinates.
2. The reference direction is the positive x axis of Cartesian coordinates.

Description of the Algorithm

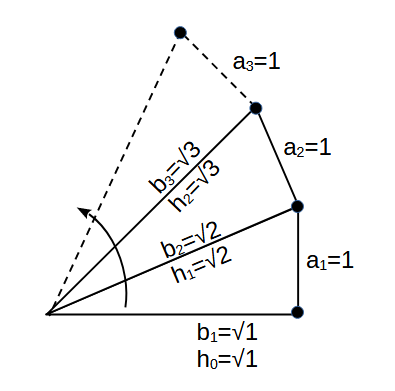
• the spiral's points are shown as small black circles.
• the diagram shows how the hypotenuse of one triangle becomes side 'b' of the next triangle.
• the starting (initial) triangle is just the line b₁. (it is a special case.)
• a triangle's sides 'a' and 'b' can be used to calculate the triangle's hypotenuse (e.g. sqrt(a**2 + b**2))
• a triangle's sides 'a' and 'b' can be used to find the triangle's interior angle. (e.g. arcsin(a/b))
• a hypotenuse and an angle can be used to create polar coordinates for each point
• to create a point's polar coordinates, use the hypotenuse and the sum of the angles of the triangles that came before it.