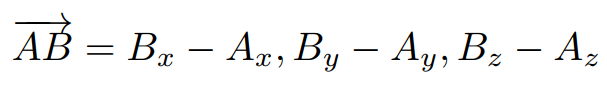What is a normal vector?
A normal vector is a vector perpendicular to a surface (3D) or
a line (2D). If the surface or line is curved, it is perpendicular
at a specific point. If the surface is flat or the line is straight,
the normal vector is perpendicular everywhere.
So what is a normal vector good for?
In computer graphics, an object can be made of many small surfaces
(triangles, rectangles, ...). When drawing a solid object, it would
speed things up to not draw (rendered) hidden surfaces. A normal
vector to a flat surface can be used to determine if that surface
is pointed towards the viewer or away from the viewer. For solid
objects, a surface pointing away from the viewer can not be seen,
and does not need to be drawn (rendered).
For example, if the viewer is at infinity on the +Z axis, a normal
vector's +z value means the surface is pointer toward the viewer
and should be drawn (rendered). A -z value means the surface is
pointed away from the viewer and will not be drawn (rendered).
if z = 0, the surface is sideways to the viewer and may or may
not be seen by the viewer. It depends on the thickness of the
object the surface represents. In many cases it is not seen (drawn)
because it is infinitely thin.
How do I order the three points to make them clockwise
for this function?
Pretend you are outside of a solid object looking down on one of
its surfaces. Select 3 points in clockwise order and list them
in order. For example:
Given the following points on the plane of the object's surface ...
+-------------------------------+
| |
| p0 p2 p5 |
| |
| p4 p3 |
| |
| p6 |
| |
+-------------------------------+
Create a clockwise list of 3 points ...
p0,p3,p6 or p2,p5,p3 or p4,p2,p5 or p3,p6,p4 or ...
Notes:
- Normal vectors are created/calculated so they point away from
an object and not into an object. Pick the "right" three points
on a surface (in clockwise direction)
to see which direction the normal vector points.
- Using your left hand to show the direction of the normal
vector. Curl your fingers (clockwise) over the points
used. Your thumb points in the direction of the normal
vector (towards or away from the viewer).
- The easiest way to get three points on the surface is to use
the object's corner points.
Vector Equation (point A to point B)
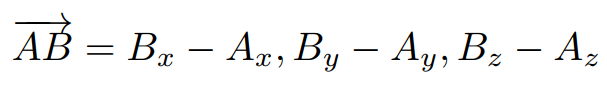
File: normal_vector.py
#! /usr/bin/python3
# ===================================================================
# Three points can define a plane. If they do, you can calculate
# a vector perpendicular to the plane. If the points do not form
# a plane the cross product vector is [0,0,0].
#
# The vector can be used to determine if a plane is facing the
# viewer or not. With solid object made up of thousands triangles,
# you can determine which triangles need to be rendered and which ones
# do not. This can make rendering the object more efficient.
# You don't need to draw all of the triangles.
# ===================================================================
import numpy as np
def calc_cross_product(p1,p2,p3,verbose=False):
if verbose:
print(f'p1 = {p1}')
print(f'p2 = {p2}')
print(f'p3 = {p3}')
# ---- get two vectors - origin point p1
v1 = [p3[0]-p1[0],p3[1]-p1[1],p3[2]-p1[2]]
v2 = [p2[0]-p1[0],p2[1]-p1[1],p2[2]-p1[2]]
if verbose:
print(f'v1 (p1-p2) = {v1}')
print(f'v2 (p3-p2) = {v2}')
# ---- the cross product is a vector perpendicular to the plane
cp = np.cross(v1,v2)
if verbose:
x = cp[0]
y = cp[1]
z = cp[2]
print(f'cross product = [ x={x},y={y},z={z} ]')
return cp
# -------------------------------------------------------------------
# ---- main
# -------------------------------------------------------------------
if __name__ == '__main__':
import sys
def test_cross_product(p1,p2,p3,title=None):
print()
print('------------------------------------------')
if title is not None:
print(title)
cp = calc_cross_product(p1,p2,p3,True)
print(f'cross product: {cp}')
if cp[0] == 0 and cp[1] == 0 and cp[2] == 0:
print(f'no normal vector')
elif cp[2] > 0:
print(f'normal vector points towards the viewer')
else:
print(f'normal vector points away from the viewer')
print('------------------------------------------')
print()
print('===================================================')
print('POINTS THAT DEFINE A PLANE')
print('viewer is at +z infinity')
print()
print('The Normal vector from a surface points toward')
print('the viewer when the points used in the calculation')
print('appear in a clockwise order.')
print('===================================================')
p1 = [3,-3,0]
p2 = [-3,0,0]
p3 = [0,3,0]
test_cross_product(p1,p2,p3,'xy plane - clockwise')
##test_cross_product(p3,p1,p2,'xy plane - clockwise')
##test_cross_product(p2,p3,p1,'xy plane - clockwise')
test_cross_product(p3,p2,p1,'xy plane - counter clockwise')
##test_cross_product(p1,p3,p2,'xy plane - counter clockwise')
##test_cross_product(p2,p1,p3,'xy plane - counter clockwise')
p1 = [0,0,3]
p2 = [-3,3,-3]
p3 = [3,3,0]
test_cross_product(p1,p2,p3,
'xyz plane slanted towards viewer - clockwise')
##test_cross_product(p3,p1,p2,
## 'xyz plane slanted towards viewer - clockwise')
##test_cross_product(p2,p3,p1,
## 'xyz plane slanted towards viewer - clockwise')
test_cross_product(p3,p2,p1,
'xyz plane slanted towards viewer - counter clockwise')
##test_cross_product(p1,p3,p2,
## 'xyz plane slanted towards viewer - counter clockwise')
##test_cross_product(p2,p1,p3,
## 'xyz plane slanted towards viewer - counter clockwise')
p1 = [3,3,3]
p2 = [0,0,0]
p3 = [-3,-3,-3]
test_cross_product(p1,p2,p3,
'straight line - clockwise')
test_cross_product(p2,p2,p1,
'straight line - counter clockwise')