Math Equations in Html

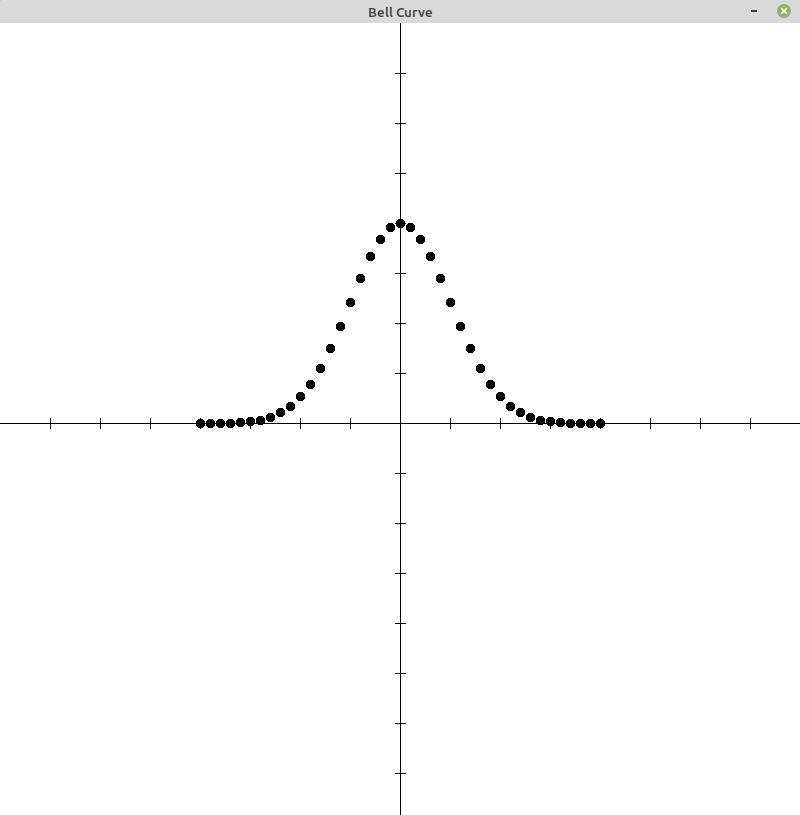
Bell Curve

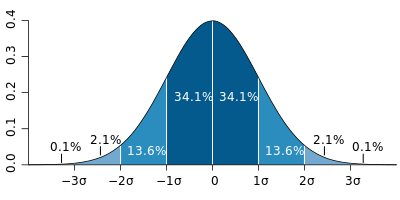
Standard Deviation
From: commons.wikimedia.org

Project #1 - Plot a Bell Curve

Using graphics.py, plot a bell curve.

plot X = -200 to 200 incremented by 10
with YMAX = 200
and a standard deviation of 50 (σ)

Vary these values and see what you get.

Are there other Python modules that can plot data?

Project #2

Create a file containing population data that is a bell curve. This file can act as population data when generating statistics. (see project #3)

generate 1000 to 3000 data points
data values should be integers
data values should be one per line

What does random.normal() do?
What does numpy.random.normal() do?
What does scipy.stats.norm() do?

Project #3 - Mean (average) and Standard Deviation

Create an interactive program to

ask the user for a population data file
read population data from a file (see project #2)
calculate the population's mean and standard deviation
display the population's mean and standard deviation
Loop...
- ask the user for a sample size
- create a random sample from the population
- calculate the sample's mean and standard deviation
- display the sample's mean and standard deviation

There are several Python modules that will generate the mean and standard deviation from a list of numbers. (see numpy)

Equation for the X,Y Coordinates of a Bell Curve

Y = Ke^{-(X-M)²/(2σ²)}

X,Y	are the curve's x,y coordinates (used for plotting, etc.)
K	is the maximum Y coordinate; used to scale the Y coordinates (height in Y units)
M	is the curve's mathematical mean (X coordinate of the mean)
σ	is the curve's standard deviation; determines how fat or skinny the curve is (width in X units)
e	is Euler's number; is a constant; is an irrational number (defined in the Python numpy module and other libraries)

From: math.stackexchange.com

With this equation the user can:

select what part of the curve to calculate; (used for plotting, etc.)
set X coordinate for the curve's mean
set maximum value of the curve's Y coordinates
set how fat of skinny the curve is; standard deviation (in X units)

Mean

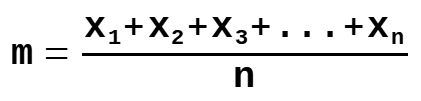m = the population mean n = the size of the population x = each value from the population

Standard Deviation

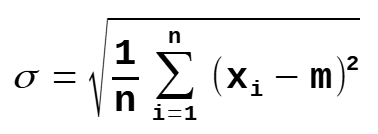σ = population standard deviation n = the size of the population x = each value from the population m = the population mean

Python Examples

# ------------------------------------------------------------------- # ---- return the bell curve's y coordinate for a given x coordinate # ---- x bell curve x coordinate # ---- ymax bell curve data arithmetic mean (y coordinate) # ---- mean bell curve data arithmetic mean (x coordinate) # ---- sd bell curve data standard deviation # ------------------------------------------------------------------- import numpy as np def BellCurveValue(x,ymax,mean,sd): y = ymax * pow(np.e,-pow(x-mean,2)/(2.0*sd*sd)) return y

# ------------------------------------------------------------------- # ---- return a list of random samples from a population list # ---- poplst - population data list # ---- samsiz - size of sample # ------------------------------------------------------------------- # ---- What kind of sampling does your problem require? # ---- When a sample is drawn from a finite population and is # ---- returned to that population, sampling is said to be # ---- "sampling with replacement". This means a sample can be # ---- selected more than once. When we sample with replacement, # ---- the two sample values are independent. For example, if we # ---- are roll a die or tossing a coin more that once, we are # ---- "sampling with replacement". # ------------------------------------------------------------------ import numpy as np import random def RandomSample(poplst,samsiz): poplen = len(poplst) # ---- collect samsiz samples sam = [] # list of samples for _ in range(samsiz): i = random.randint(0,poplen-1) sam.append(poplst[i]) # ---- calculate mean and standard deviation avg = np.mean(sam) # mean (average) std = np.std(sam) # standard deviation return (sam,avg,std)

Useful Links

Formula for the Normal Distribution or Bell Curve
Note: This has a slightly different version of the equation. Read the article for more information.

Standard Deviation (Wikipedia)

Normal Distribution (Wikipedia)

Standard deviation (simply explained) (YouTube)

FYI

Sometimes suspect/bad/outlier data can be part of a sample taken from a population. For a method to eliminate outliers, click HERE .