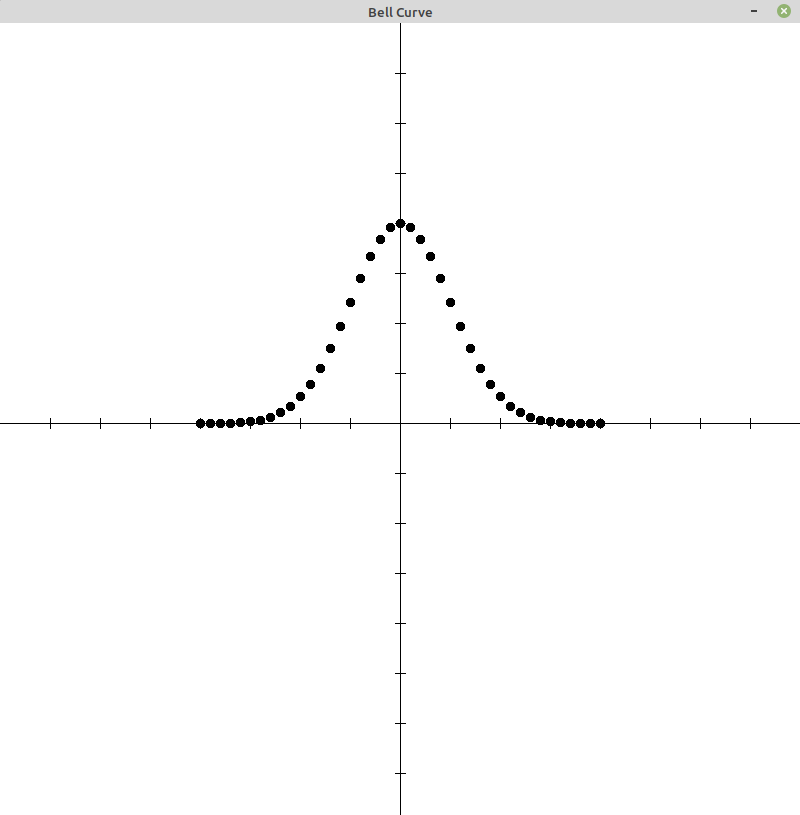
Bell Curve
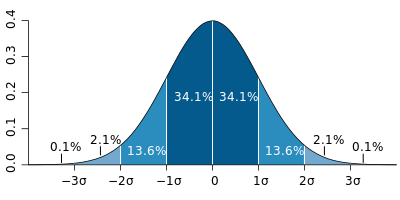
Standard Deviation
From: commons.wikimedia.org
Project #1
Use the Python Statistics Module
(Mathematical statistics functions
)
- generate a list of random numbers
- value range: integers between 0 to 29 (inclusive)
- list size: 1000
- calculate and display the mean (average), median, and mode
- calculate and display the standard deviation (
σ ) (sigma)- How many values are within 1
σ of the mean?
What percentage of the total are they? - How many values are within 2
σ of the mean?
What percentage of the total are they? - How many values are within 3
σ of the mean?
What percentage of the total are they?
- How many values are within 1
Question: What is the difference between mean and average?
Project #2
Watch the YouTube video
Particle Physics Discoveries that Disappeared.
What is the significance of 5
Project #3
Repeat Project #1, but do not use existing modules or functions. Write your own. (See equations below.)
Project #4
Create a population of random numbers that are a bell curve. (size 1000?)
Calculate and display the population's mean, median, and mode.
- Select a random sample of 100 from the population
- calculate and display the sample's mean, median, and mode
- calculate and display the sample's standard deviation (
σ )- How many values are within 1
σ of the mean?
What percentage of the total are they? - How many values are within 2
σ of the mean?
What percentage of the total are they? - How many values are within 3
σ of the mean?
What percentage of the total are they? - What are the normal/theoretical percentages for a bell curve?
How does your sample compare?
- How many values are within 1
Project #5
Plot the mean of several samples from a population. (See Project #1 and Project #3)
- loop (100 times?):
- Get a random sample (100)
- Calculate the sample's mean value
- Add the sample's mean to a list of means
- Plot the means (histogram)
(make it pretty: plot title, axis labels, tick marks, ...)
I suggest you use the pyplot or related modules.
matplotlib.pyplot (documentation and examples)
(see matplotlib.pyplot.scatter(x, y))
Equation for the X,Y Coordinates of a Bell Curve
| Y = Ke-(X-M)2/(2σ2) | |
| X,Y | are the curve's x,y coordinates (used for plotting, etc.) |
| K | is the maximum Y coordinate; used to scale the Y coordinates
(height in Y units) |
| M | is the curve's mathematical mean (X coordinate of the mean) |
| σ | is the curve's standard deviation;
determines how fat or skinny the curve is (width in X units) |
| e | is Euler's number; is a constant; is an irrational number (defined in the Python math module as a constant: math.e) |
Mean
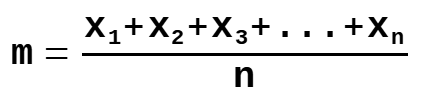m = the population mean
n = the size of the population
x = each value from the population
Standard Deviation
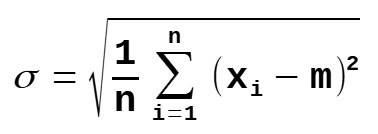σ = population standard deviation
n = the size of the population
x = each value from the population
m = the population mean
Generate a List of Random Number (sorted)
import random
# ---------------------------------------------------------------
# ---- return a list of random integers
# ----
# ---- lst_siz number of elements in returned list
# ---- lst_min minimum element value
# ---- lst_max maximum element value
# ----
# ---- note: random.randint returns a randomly generated integer
# ---- from the specified range (inclusive).
# ---------------------------------------------------------------
def random_list(lst_siz,lst_min,lst_max):
lst = []
i = 0
while i < lst_siz:
lst.append(random.randint(lst_min,lst_max))
i += 1
return sorted(lst)
What must you do to generate the same random list over and over again? (Hint: seed)
Generate Random Values That Fit A Bell Curve
#!/usr/bin/python3
# ====================================================================
# create a population of random numbers from a theoretical
# normal distribution (bell curve) - display various values and plots
#
# Note: python -n pip install scipy
# ====================================================================
import scipy.stats
import numpy as np
import matplotlib.pyplot as plt
number_of_bins = 20 # number of bins for histogram
# ---- create random number generator
rng = np.random.default_rng()
# ---- create a random list of numbers that fit
# ---- a standard distributed (bell curve)
pop = rng.normal(size=1000)
pmin = min(pop)
pmax = max(pop)
print(f'pop size = {len(pop)}')
print(f'pop min = {pmin}')
print(f'pop max = {pmax}')
# ---- plot histogram of random population
counts,bins,ignore = plt.hist(pop,bins=number_of_bins)
# ---- plot theoretical probability distribution
bin_width = (pmax-pmin)/number_of_bins
hist_area = len(pop)*bin_width
x = np.linspace(-4,4,number_of_bins+1) # x values
y = scipy.stats.norm.pdf(x)*hist_area # y values
plt.plot(x,y)
# ---- display plots
plt.show()
Click HERE
for "Non-Bell Curve Basic Statistics Examples".